DNB: A Joint Learning Framework for Deep Bayesian Nonparametric Clustering

Abstract

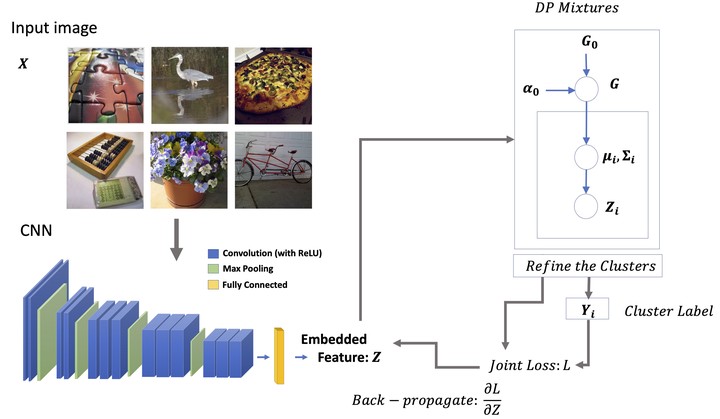
Clustering algorithms based on deep neural networks have been widely studied for image analysis. Most existing methods require partial knowledge of the true labels, namely, the number of clusters, which is usually not available in practice. In this paper, we propose a Bayesian Nonparametric framework, deep nonparametric Bayes (DNB), for jointly learning image clusters and deep representations in a doubly-unsupervised manner. In doubly-unsupervised learning, we are dealing with the problem of “unknown unknowns”, where we estimate not only the unknown image labels but also the unknown number of labels as well. The proposed algorithm alternates between generating a potentially unbounded number of clusters in the forward pass, and learning the deep networks in the backward pass. With the help of the Dirichlet process mixtures, the proposed method is able to partition the latent representations space without specifying the number of clusters a priori. An important feature of this work is that all the estimation is realized with an end-to-end solution, which is very different from the methods that rely on post-hoc analysis to select the number of clusters. Another key idea in this paper is to provide a principled solution to the problem of “trivial solution” for deep clustering, which has not been much studied in the current literature. With extensive experiments on benchmark datasets, we show our doubly-unsupervised method achieves good clustering performance and outperforms many other unsupervised image clustering methods.