Abstract
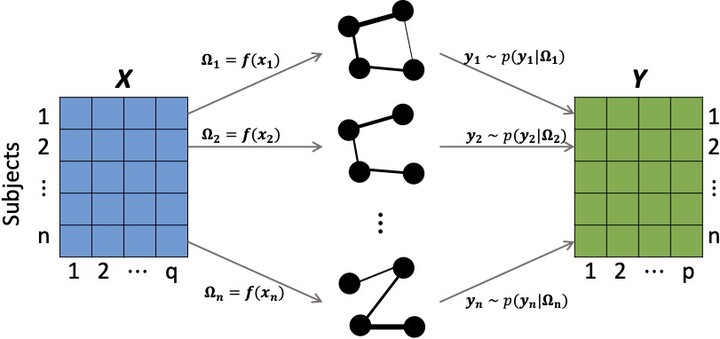
We introduce Bayesian Gaussian graphical models with covariates (GGMx), a class of multivariate Gaussian distributions with covariate-dependent sparse precision matrix. We propose a general construction of a functional mapping from the covariate space to the cone of sparse positive definite matrices, that encompasses many existing graphical models for heterogeneous settings. Our methodology is based on a novel mixture prior for precision matrices with a non-local component that admits attractive theoretical and empirical properties. The flexible formulation of GGMx allows both the strength and the sparsity pattern of the precision matrix (hence the graph structure) change with the covariates. Posterior inference is carried out with a carefully designed Markov chain Monte Carlo algorithm which ensures the positive definiteness of sparse precision matrices at any given covariates’ values. Extensive simulations and a case study in cancer genomics demonstrate the utility of the proposed model.