Covariate-Assisted Bayesian Graph Learning for Heterogeneous Data

Abstract

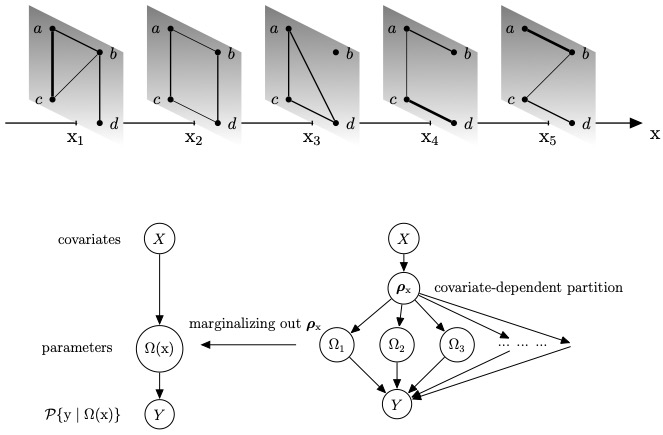
In a traditional Gaussian graphical model, data homogeneity is routinely assumed with no extra variables affecting the conditional independence. In modern genomic datasets, there is an abundance of auxiliary information, which often gets underutilized in determining the joint dependency structure. In this article, we consider a Bayesian approach to model undirected graphs underlying heterogeneous multivariate observations with additional assistance from covariates. Building on product partition models, we propose a novel covariate-dependent Gaussian graphical model that allows graphs to vary with covariates so that observations whose covariates are similar share a similar undirected graph. To efficiently embed Gaussian graphical models into our proposed framework, we explore both Gaussian likelihood and pseudo-likelihood functions. For Gaussian likelihood, a G-Wishart distribution is used as a natural conjugate prior, and for the pseudo-likelihood, a product of Gaussian-conditionals is used. Moreover, the proposed model has large prior support and is flexible to approximate any ν-Ḧolder conditional variance-covariance matrices with ν ∈ (0,1]. We further show that based on the theory of fractional likelihood, the rate of posterior contraction is minimax optimal assuming the true density to be a Gaussian mixture with a known number of components. The efficacy of the approach is demonstrated via simulation studies and an analysis of a protein network for a breast cancer dataset assisted by mRNA gene expression as covariates.