Individualized Inference in Bayesian Quantile Directed Acyclic Graphical Models

Abstract

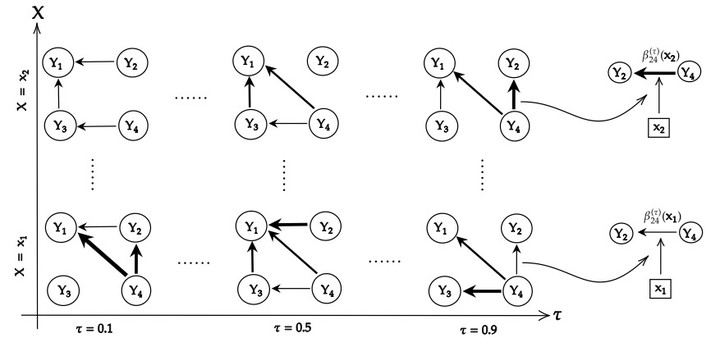
We propose an approach termed “qDAGx” for Bayesian covariate-dependent quantile directed acyclic graphs (DAGs) where these DAGs are individualized, in the sense that they depend on individual-specific covariates. A key distinguishing feature of the proposed approach is that the individualized DAG structure can be uniquely identified at any given quantile, based on purely observational data without strong assumptions such as a known topological ordering. For scaling the proposed method to a large number of variables and covariates, we propose for the model parameters a novel parameter expanded horseshoe prior that affords a number of attractive theoretical and computational benefits to our approach. By modeling the conditional quantiles, qDAGx overcomes the common limitations of mean regression for DAGs, which can be sensitive to the choice of likelihood, e.g., an assumption of multivariate normality, as well as to the choice of priors. We demonstrate the performance of qDAGx through extensive numerical simulations and via an application in precision medicine by inferring patient-specific protein–protein interaction networks in lung cancer.